ENZYMES - MICHAELIS-MENTON KINETICS

How can we describe the kinetics of such a reaction quantitatively in terms of parameters that can be measured easily? The model developed by Leonor Michaelis and Maud Menten a century ago does this. Its value lies in the facts that the assumptions underlying their model are simple enough to yield equations that are easy to manipulate, yet realistic enough to allow accurate quantitative predictions of useful features of catalyzed reactions in a clinical setting; e.g., the effects of drugs that act as competitive inhibitors. Here, we will briefly show how the equation is developed from these basic assumptions as a way of understanding these applications.
An additional assumption is that [S] is much greater than [E] (a plausible assumption for most enzymes in human cells), so the concentration of free substrate, [S], is essentially equal to the total substrate concentration. From this assumption and the ones about rates of the individual steps of the process comes the crucial steady-state assumption: as the reaction gets underway, a steady state is quickly reached in which the rate of formation of enzyme-substrate complex by binding of E and S is equal to the rates of loss of the complex by dissociation to re-form E and S and by reaction to form E and P. The model only considers reactions under conditions where little product has accumulated so, even if a reaction is chemically reversible, formation of ES by the reverse reaction can be ignored. (Note that this “little product” restriction is generally physiologically realistic: the individual reactions we will consider are parts of larger processes, so as fast as product is formed by one reaction, it is consumed by following ones. Indeed, we will often see that accumulation of a product functions as a signal to shut down the overall process.) These assumptions allow the derivation of the Michaelis-Menten equation:
A strong association between a substrate and an enzyme is reflected in a low KM value; a weaker association is reflected in a larger KM value; an enzyme with a low KM value is thus likely to be able to act on a substrate even when substrate concentrations are low, while one with a high KM value is likely to be active only when substrate concentrations are high. We will see that this provides a useful way of characterizing the various protein channels responsible for cellular glucose uptake and understanding their distinctive roles in various physiological states in the body.
The significance of KM in graph at the start of this section now also is clear. Unlike the individual rate constants, the value of KM can be measured. It has units of moles/liter, and equals the concentration of substrate needed for the reaction to proceed at half its maximum velocity.
What about reactions involving more than one substrate, like the hydrolysis of a peptide bond? In the test tube, this situation can be handled by keeping the concentration of one substrate constant while allowing the other to vary. This process is described as measuring the KM of the enzyme with respect to the variable substrate. This strategy has relevance in the body as well: we will encounter many cases in which one of the substrates of a reaction of interest is indeed nearly constant under physiological conditions while that of a second substrate can vary widely. The water needed for that hydrolysis reaction, for instance, it present at a constant high concentration in the body.
One more piece of algebra is useful for describing quantitative properties of enzymes that show Michaelis-Menten kinetics. Taking the inverse of both sides of the Michaelis-Menten equation yields the Lineweaver-Burk equation.

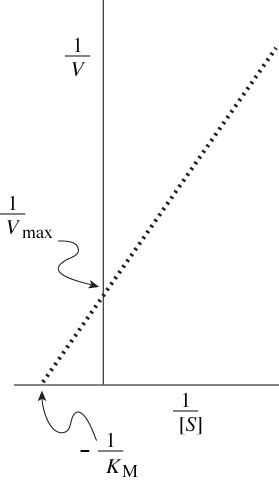
With the equation in this rearranged form, Vmax and KM values for an enzyme can be calculated from measurements of reaction rates at various substrate concentrations by simple linear extrapolation. More important for our purposes, this way of visualizing rate data provides an easy way of distinguishing two important kinds of enzyme inhibitors, competitive ones and noncompetitive ones.
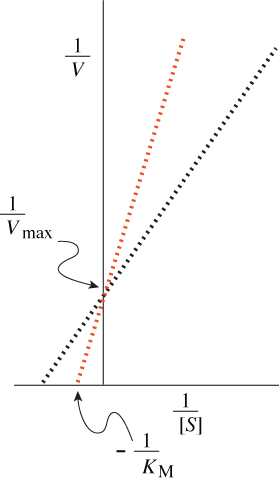
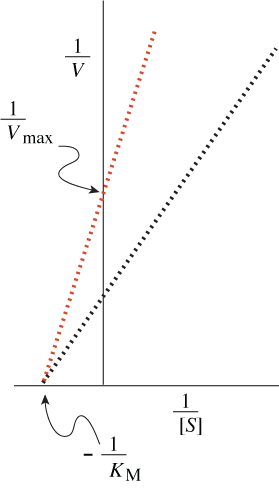
A non-competitive inhibitor, in contrast, binds to a site on the enzyme distinct from the enzyme’s active site. Inhibitor binding has no effect on the affinity of enzyme for substrate, but causes a conformational change in the enzyme that prevents it from catalyzing the conversion of bound substrate to product. Otherwise, binding of inhibitor and substrate are independent events, and no amount of substrate binding can dislodge inhibitor molecules from their site on the enzyme. Rather, the rate of dissociation of enzyme-inhibitor complexes is determined only by the affinity of the enzyme for the inhibitor. Consequently, the KM of enzyme for substrate is unchanged in the presence of a noncompetitive inhibitor, but the apparent Vmax of the reaction is reduced. In effect, while in the absence of inhibitor all enzyme molecules are available to act on substrate, in the presence of a noncompetitive inhibitor only some of them are available. The result is shown as a Lineweaver-Burk plot in the diagram.